Historia de la Raíz Cuadrada de dos

Las raíces cuadradas son expresiones matemáticas que surgieron al plantear diversos problemas geométricos como la longitud de la diagonal de un cuadrado. El Papiro de Ahmes datado hacia 1650 a. C., que copia textos más antiguos, muestra cómo los egipcios extraían raíces cuadradas.En la antigua India, el conocimiento de aspectos teóricos y aplicados del cuadrado y la raíz cuadrada fue al menos tan antiguo como los Sulba Sutras, fechados alrededor del 800-500 a. C. (posiblemente mucho antes). Un método para encontrar muy buenas aproximaciones a las raíces cuadradas de 2 y 3 es dado en el Baudhayana Sulba Sutra. Aryabhata en su tratado Aryabhatiya (sección 2.4), dio un método para encontrar la raíz cuadrada de números con varios dígitos.

Los babilonios aproximaban raíces cuadradas haciendo cálculos mediante la media aritmét ica,

 

Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que la raíz cuadrada de  era irracional (inconmensurable) o no expresable como cociente alguno, lo que supuso un hito en la matemática de la época.

Posteriormente se fue ampliando la definición de raíz cuadrada. Para los números reales negativos, la generalización de la función raíz cuadrada de éstos da lugar al concepto de los números imaginarios y al cuerpo de los números complejos, algo necesario para que cualquier polinomio tenga todas sus raíces (teorema fundamental del álgebra). La diagonalización de matrices también permite el cálculo rápido de la raíz de una matriz.

Inicialmente mostraron su utilidad para la resolución de problemas trigonométricos y geométricos, como la diagonal de un cuadrado o el teorema de Pitágoras. Posteriormente fueron ganando utilidad para operar con polinomios y resolver ecuaciones de segundo grado o superior, siendo una de las herramientas matemáticas más elementales hoy en día.

David Eugene Smith, en History of Mathematics, dice acerca de la situación existente:

"En Europa esos métodos (para encontrar el cuadrado y la raíz cuadrada) no aparecieron antes de Cataneo (1546). Él dio el método de Aryabhata para determinar la raíz cuadrada".⁴

Según Julio Rey Pastor y José Babini, Catald calcula en 1613 raíz cuadrada aproximando por fracciones continuas, como aparece en la obra común Historia de la Matemática.

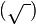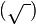El símbolo de la raíz cuadrada  fue introducido en 1525 por el matemático Christoph Rudolff para representar esta operación^5 6que aparece en su libro Coss, siendo el primer tratado de álgebra escrito en alemán vulgar. El signo no es más que una forma estilizada de la letra r minúscula para hacerla más elegante, alargándola con un trazo horizontal, hasta adoptar el aspecto actual, que representa la palabra latina radix, que significa raíz. También se conjetura que pudiese haber surgido de la evolución del punto que en ocasiones se usaba anteriormente para representarlo, donde posteriormente se le habría añadido un trazo oblicuo en la dirección del radicando.

Tiempo atrás, varios matemáticos vieron la necesidad de idear números que representasen la raíz cuadrada de números negativospara poder resolver todas las ecuaciones de segundo grado, pero no será hasta 1777 cuando Euler simbolice la raíz cuadrada de -1 con la letra i, dando así cabida al desarrollo de los números complejos.

Utilidad de la Raíz Cuadrada de dos

La gráfica de la función  es una semiparábolacon directriz vertical.

La raíz cuadrada permite definir una función real sobre los números no negativos, para cada número real x esta función se define como el único número no negativo y que elevado al cuadrado es igual a x. Consiste en hallar el número del que se conoce su cuadrado. La función raíz cuadrada de x se expresa equivalente de las siguientes maneras:

Usualmente la raíz cuadrada de un número entero no es un número racional a menos que el número entero sea un cuadrado perfecto, como por ejemplo:

ya que:

El descubrimiento de que la raíz cuadrada de muchos números era un número irracional se atribuye a los pitagóricos. Los babilonios y egipcios ya disponían de medios de estimar numéricamente la raíz cuadrada, pero su interés parece haber sido eminentemente práctico por lo que no parecen existir referencias sobre la naturaleza de la raíz cuadrada y el problema de si esta podía ser expresada como cociente de dos números enteros.

La relación entre la matemática y estadística

La estadística matemática es escala previa en el estudio de la estadística desde un punto de vista puramente formal, usando la teoría de la probabilidad y otras ramas de la matemática tales como álgebra lineal y análisis matemático. La estadística matemática trata de la obtención de información a partir de los datos. En la práctica tales datos contienen cierta aleatoriedad o incertidumbre. La estadística trabaja con estos datos usando los métodos de la teoría de la probabilidad.

La estadística matemática se divide en:

• Estadística descriptiva: parte que se encarga de describir los datos, esto es, de realizar un resumen y describir sus propiedades típicas.

• Inferencia estadística: parte que elabora conclusiones a partir de una muestra de los datos, en otras palabras, comprueba el ajuste de los datos a determinadas condiciones y proporciona una medida de la bondad de los mismos en términos probabilísticos.

La estadística matemática es la base teórica para muchas prácticas en la estadística aplicada.

La estadística es una rama de la matemática porque

ESTADÍSTICA: Ciencia o una rama de las matemáticas

Encontrar un concepto clave que englobe todas las características que tiene la estadística no ha sido fácil. En 1935 W. F. Willcox reunió 115 definiciones y aportó una más para sustituirlas, sin lograrlo.
Según M. G. Kendall definir en que consiste o qué es la estadística ha sido una materia que ha dividido a lo largo de la historia a los propios estadísticos. Hay autores que la consideran como “la reina de las ciencias” (Quetelet), hasta otros que la consideran como “una técnica más de las matemáticas” ( Gini, 1953).
Es por eso que en este discurso, mas que encontrar una definición global de estadística, se hará hincapié a establecer si la estadística es una ciencia o una rama de las matemáticas, puesto que, para mi como futuro profesor de matemáticas es esencial conocer en profundidad los contenidos a desarrollar en el aula de clases, debido a que la nueva reforma curricular establece que el docente construya un conocimiento acorde a las sociedades globalizadas, para que los estudiantes puedan tener una formación apta a los nuevos tiempos.
Cuando popularmente se habla de estadística se tiende a relacionarla con datos numéricos, porcentajes, gráficos, tablas, fórmulas y, más aún, netamente relacionadas con las matemáticas. Esto es, debido ha, que durante la enseñanza media; en especial 1º y 2º año, la reforma educacional establece una formación general que implica un mínimo de conocimientos establecidos, tanto a colegios particulares, particulares subvencionados y municipales. Es aquí donde la estadística se da a conocer dentro de la asignatura de matemática, como una forma de calcular probabilidades y todo lo referente a esa unidad ( gráficos, porcentajes, etc.), es por eso que las personas tienden a confundir estadística con las matemáticas; además los medios de comunicación nos abordan diariamente con información relevante a la estadística, lo que implica que las personas se formen un concepto erróneo de ella, que A. Piatier definió como “ definiciones humorísticas”.
Solo cuando nos adentramos al campo de la investigación de las ciencias sociales (medicina, biología, psicología, etc.), empezamos a percibir que la estadística no solo es algo más que números y probabilidades; sino que se convierte en una herramienta fundamental que permite obtener beneficios en cualquier tipo de estudio.
Si consideramos la hipótesis que la estadística es una rama de las matemáticas, aparece la siguiente interrogante: ¿ Cómo la estadística puede ayudar a estudiar otras ciencias, si sólo es una rama de las matemáticas?. Esto llevó a que Murria R. Spiegel en 1991 propusiera que: “la estadística estudia los métodos científicos para recoger, organizar, resumir, y organizar datos, así como para sacar conclusiones válidas y tomar decisiones razonables en tal análisis”. Esto sin duda estableció los tópicos que dan lugar que la estadística no es una rama de las matemáticas. Esto permitió que más adelante Gonzalo Sánchez-Crespo y Vicente Manzano A. Definieran la estadística como: “Ciencia que se ocupa del estudio de fenómenos de tipo genérico, normalmente complejos y enmarcados en un universo variable, mediante el empleo de modelos de reducción de la información y de análisis de validación de los resultados en términos de representatividad.”

Hoy en día, si bien no existe una definición exacta de estadística, esta claro que es considerada una ciencia por el rol que cumple, y los aportes que realiza a todas las demás ciencias. No obstante, es claro señalar que esta muy relacionada con las matemáticas en cuanto a los procedimientos que utiliza, pero que tiene objetivos y finalidades distintas.

La utilidad de la matemática en la salud

  La matemática médica o matemática médica y biológica es un campo interdisciplinario de la ciencia en el cual las matemáticas  explican fenómenos, procesos o eventos asociados a la medicina  o a la biología. Estos  pueden ser utilizados en el análisis o solución de problemas pertenecientes al área de las ciencias de la salud o de la medicina. Muchos métodos matemáticos han resultado efectivos en el estudio de problemas de salud.

Con esto se procura el desarrollo de la matemática "hacia la salud", es decir, hacia el ámbito del proceso salud-enfermedad. Y, en menor grado, "hacia dentro", o sea, hacia el desarrollo de las matemáticas mismas.

La matemática aplicada es usada frecuentemente en distintas áreas de la medicina.

Por ejemplo:  Estadística de la salud, en la bioestadística. Cálculo de variaciones, al cálculo de desviaciones respecto a la media en mensuraciones de la clínica.

Att:
Adelmary Carrillo.